目次
座標系の平行移動
平行移動の方法
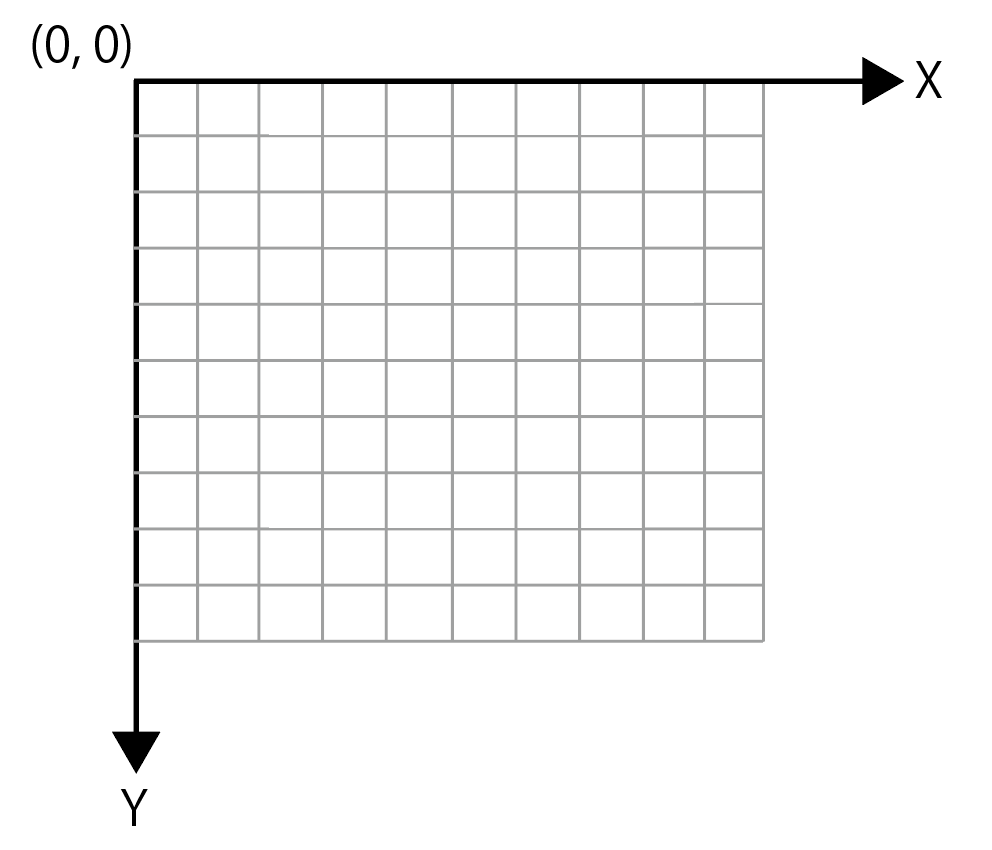
Processingのウィンドウは一枚の方眼紙のように機能します。下図のような座標系をイメージすると理解しやすいです。Processingでは表示画面の左上に原点(0, 0)があります。Y軸が下向きであることに注意してください。
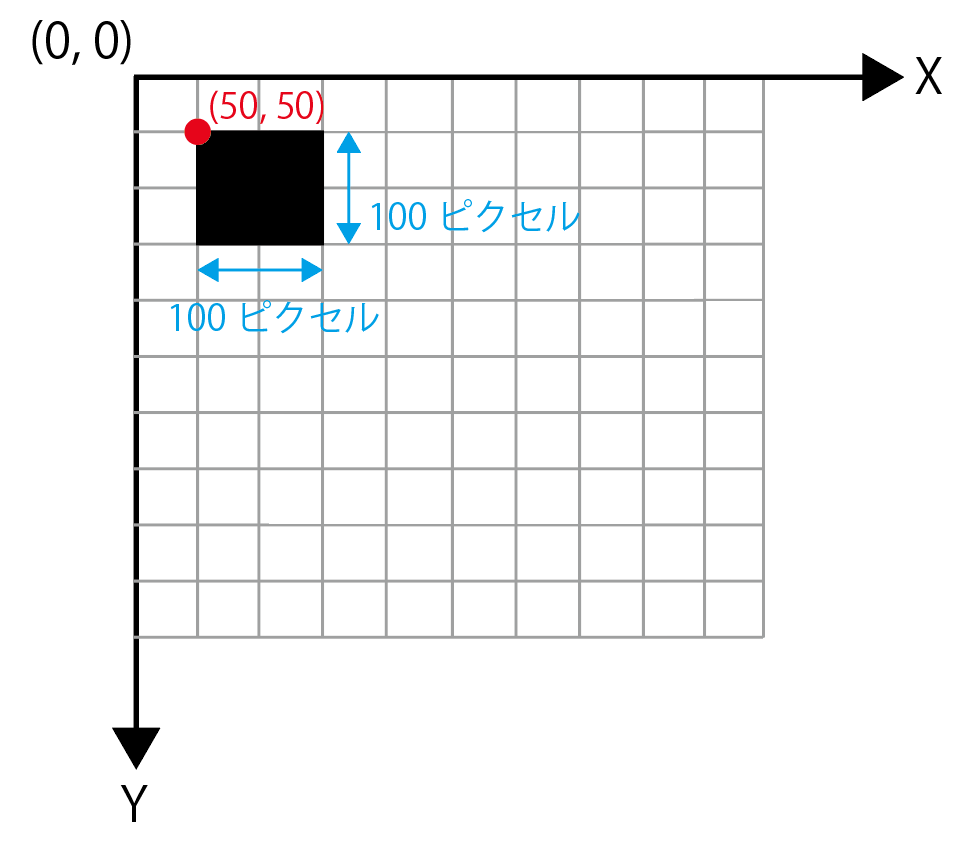
単純な四角形を描画したいときには、この方眼紙上の座標を指定します。例えば、(50, 50)の位置から、幅100ピクセル、高さ100ピクセルの四角形を描画したければ、rect関数を使って次のように指定します。
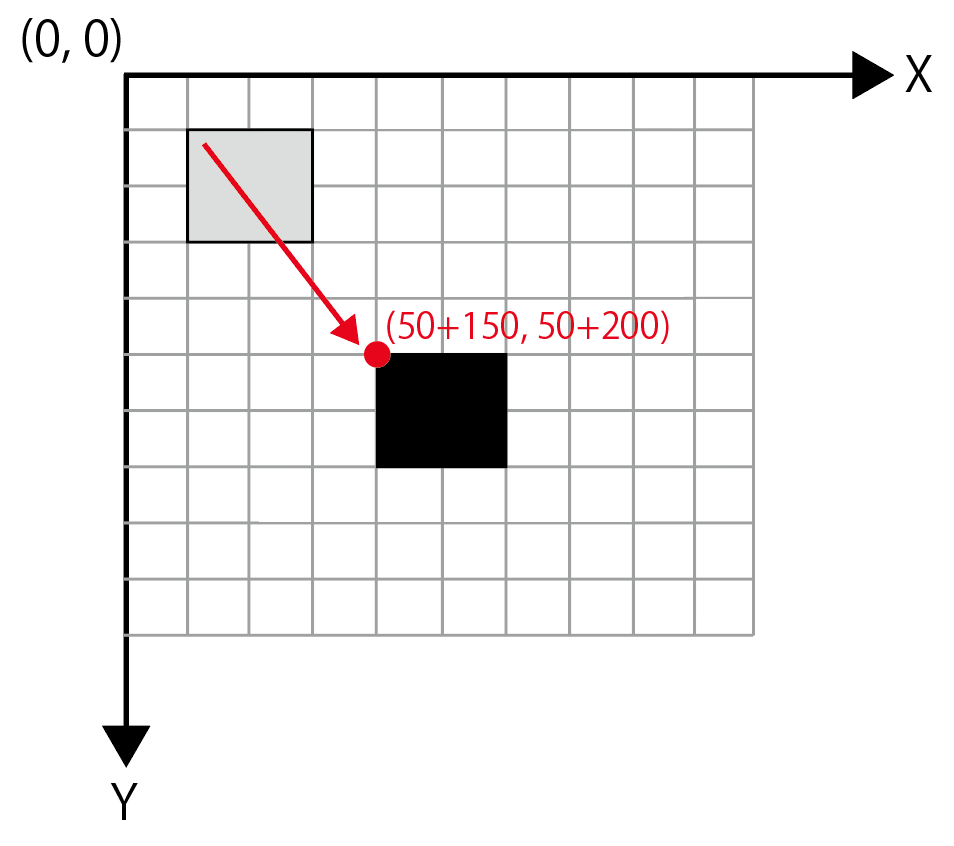
この四角形をX軸方向に150ピクセル、Y軸方向に200ピクセル移動したい場合、ひとつの解決策はrect関数の引数を次のように変えることです。
次に、もうひとつの解決策を示します。rect関数の引数を変えるのでなく、座標系(方眼紙)そのものを移動するというものです。座標系をX軸方向に150ピクセル、Y軸方向に200ピクセル移動することで、全く同じ結果を得ることができます。
座標系の平行移動は「translate関数」を使って、次のように簡単に行えます。引数で座標系の移動量を指定しています。
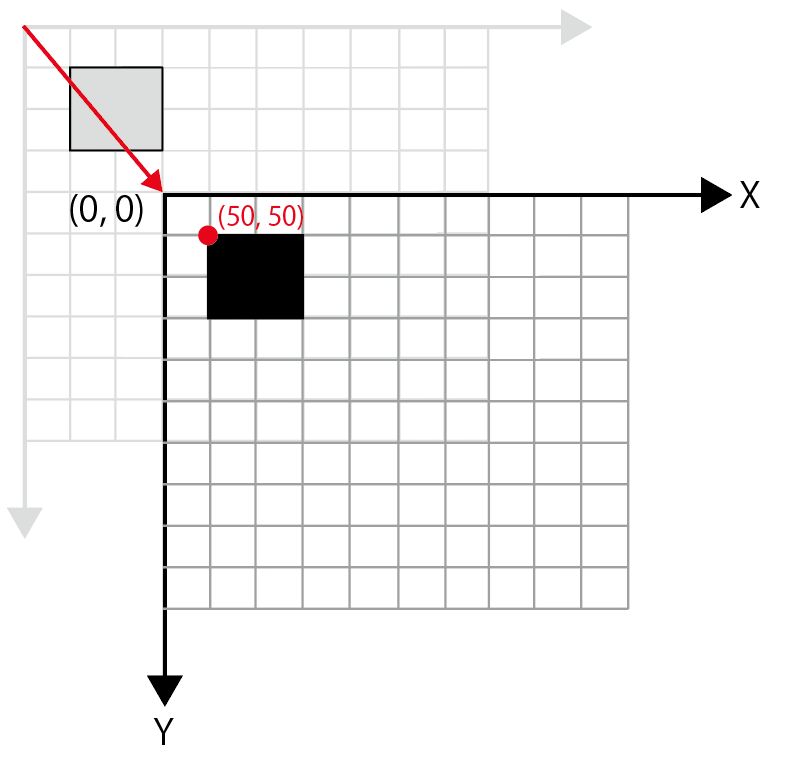
四角形の左上の点(赤い点)の位置座標が(50, 50)のまま変わっていないことに注意してください。ここで移動したのはあくまでも「座標系のみ」です。
平行移動のサンプルコード
座標系を平行移動するサンプルコードとその実行結果を示します。9行目で基準となるグレーの四角形を描いています。13行目と18行目では、グレーの四角形を、X軸方向に150ピクセル、Y軸方向に200ピクセル移動した四角形をそれぞれ描画しています。
13行目では、rect関数の引数を変えることで、四角形の移動を行なっています。この四角形は赤線で表現されます。
17行目でtranslate関数を使って、座標系をX軸方向に150ピクセル、Y軸方向に200ピクセル移動ています。その後、18行目で四角形を描画しています。この四角形は青く塗りつぶされて表現されます。赤い線の四角形と位置が一致していることから、座標系の移動でも同様の結果が得られたことが分かります。このことから、translate関数を使って座標系の移動しても、オブジェクトの移動が可能なことが理解できたと思います。
コード
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | void setup() { size(500, 500); smooth(); background(255); noStroke(); fill(192); rect(50, 50, 100, 100); stroke(204,0,0); strokeWeight(4); rect(50+150,50+200,100,100); fill(0, 0, 255, 128); noStroke(); translate(150, 200); rect(50, 50, 100, 100); } |
実行結果

座標系を移動すると何が良いか?
先ほどの簡単な例では、translate関数で座標系を移動するメリットをあまり感じられなかったかもしれません。そこで次のようなコードを考えてみます。これは家の列を描画するコードです。4行目のfor構文で家を描くX位置を変化させて、6行目でhouse関数を呼び出しています。house関数では、三角形と四角形を組み合わせて、家の形を表現しています。
コード
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | void setup() { size(500, 200); for (int i = 10; i < 400; i +=50) { house(i, 20); } } void house(int x, int y) { fill(91,66,61); triangle(x + 15, y, x, y + 15, x + 30, y + 15); fill(0,100,255); rect(x, y + 15, 30, 30); fill(255,255,255); rect(x + 15, y + 30, 10, 15); } |
実行結果

このコードを、先ほどの四角形の例を参考にして、translate関数を使って書きかえてみます。13行目にtranslate関数を追加したことで、14行目〜19行目からパラメータXとYをなくすことができて、コードが先ほどよりもすっきりしたと思います。12行目と20行目に「pushMatrix」と「popMatrix」という関数の呼び出しを追加していることにも注意してください。「pushMatrix」でその時点(translate実行前)の座標系の情報を保存して、「popMatrix」で保存した座標系の情報を取り出しています。つまり、translate実行前の座標系に戻しているということです。
コード
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | void setup() { size(500, 200); for (int i = 10; i < 400; i +=50) { house(i, 20); } } void house(int x, int y) { pushMatrix(); translate(x, y); fill(91, 66, 61); triangle(15, 0, 0, 15, 30, 15); fill(0, 100, 255); rect(0, 15, 30, 30); fill(255, 255, 255); rect(15, 30, 10, 15); popMatrix(); } |
実行結果

座標系の回転移動
回転移動の方法
座標系(方眼紙)を平行移動するだけなく、rotate関数を使って回転移動させることもできます。例えば、45°回転させたければ、rotate関数を使って、次のようにします。
ここで、角度をラジアンで指定する必要があることに注意してください。Processingのradians関数を使うことで、引数として指定した「度」を「ラジアン 」に変換することができます。また、「ラジアン 」を「度」に変換するdegreeという関数もあります。
下図のような四角形を45°回転させることを考えます。

rotate(radians(45))を実行した後に、四角形を描画すると次のようになります。
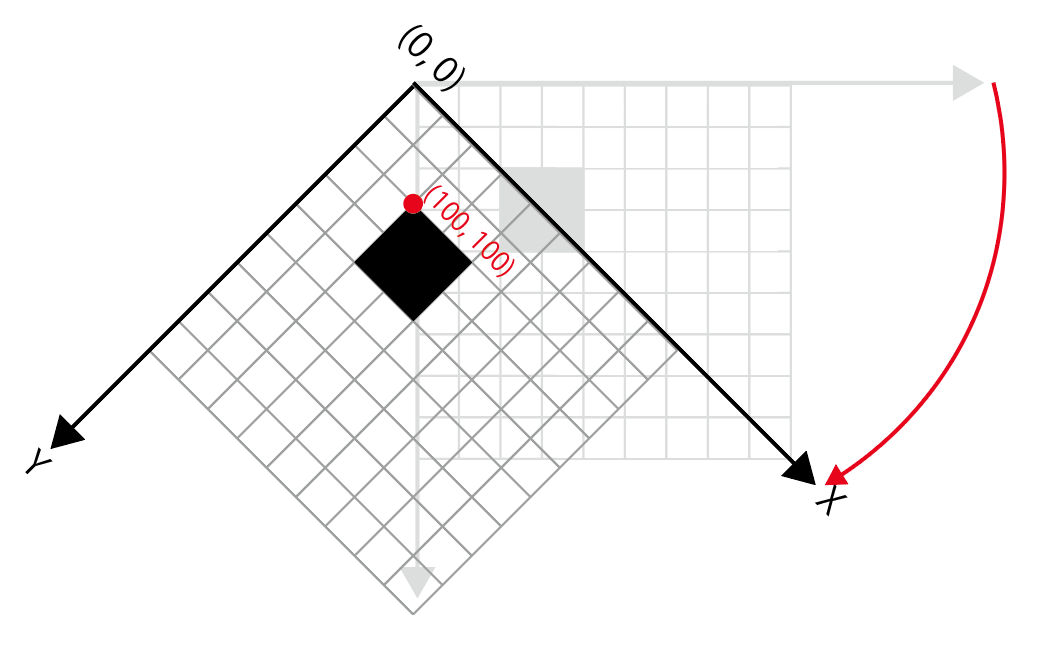
translateのときと同じように、四角形の左上の点の位置座標が(100, 100)のまま変わっていないことに注意してください。移動したのはあくまで「座標系のみ」です。
確かに座標系を回転させることができましたが、四角形を回転させるイメージとは少し異なる実行結果だったかもしれません。なぜでしょうか?それは回転の基準点を特に指定しなかったからです。回転の基準点を任意の位置に平行移動させるには、translate関数を使います。
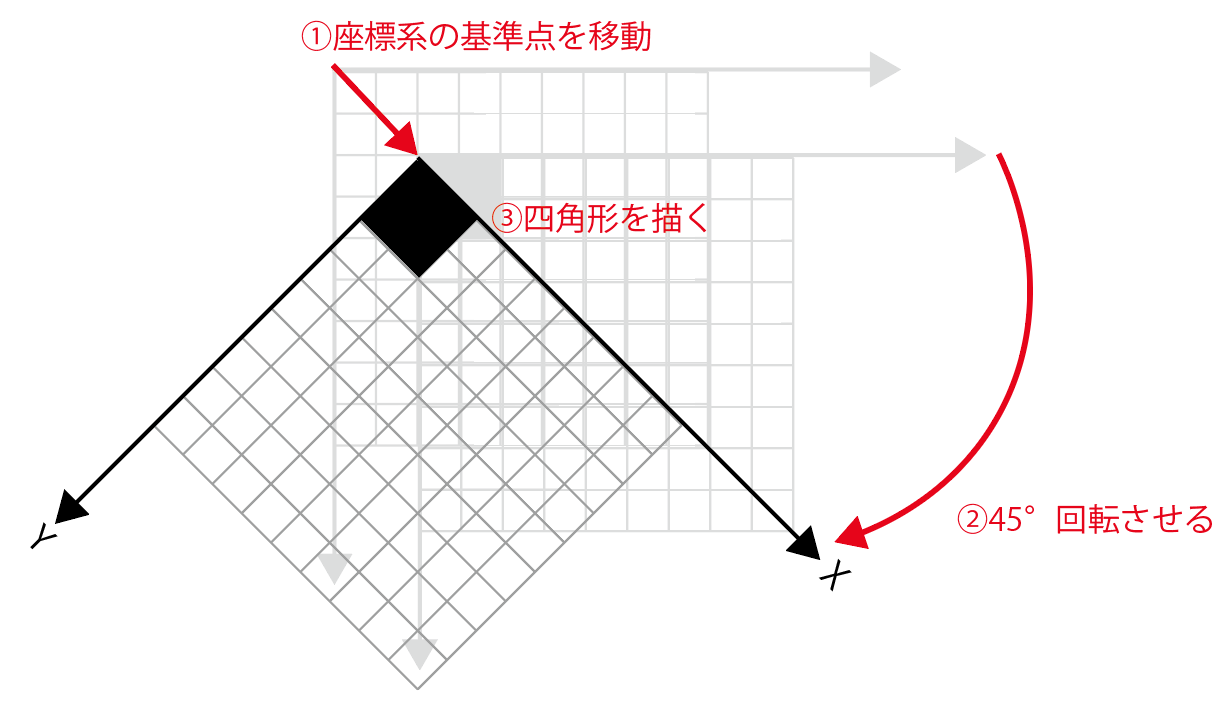
四角形を回転させる手順は次の通りです。
- 座標系の基準点(0, 0)を、回転の中心としたい位置(100, 100)に移動
- 座標系をπ/4ラジアン(45°)回転させる
- 座標系の基準点(0, 0)に四角形を描く
この手順を図示すると、下図のようになります。
回転移動のサンプルコード
座標系を回転移動するサンプルコードとその実行結果を示します。8行目で基準となるグレーの四角形を描いています。このサンプルでは基準点の移動は行わずに、11行目でそのまま座標系の回転を行なっています。回転の基準点は表示画面の左上となっているので、実行結果では半分にかけた黒い四角形が表示されています。
コード
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | void setup() { size(500, 500); background(255); smooth(); fill(192); noStroke(); rect(100, 100, 100, 100); pushMatrix(); rotate(radians(45)); fill(0); rect(100, 100, 100, 100); popMatrix(); } |
実行結果

次に、基準点を移動してから座標系を回転させるサンプルコードとその実行結果を示します。11行目にtranslate関数を追加して、座標系の基準点を平行移動しています。これに合わせて、14行目のrect関数の引数を変更しています。座標系の基準点を移動しているので、四角形を描く位置は(0, 0)になっています。実行結果を確認すると、グレーの四角形の左上の点を基準として、黒い四角形が45°回転されていることが分かります。
コード
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | void setup() { size(500, 500); background(255); smooth(); fill(192); noStroke(); rect(100, 100, 100, 100); pushMatrix(); translate(100,100); rotate(radians(45)); fill(0); rect(0, 0, 100, 100); popMatrix(); } |
実行結果

まとめ
今回はProcessingの「座標系の平行移動・回転移動」について扱いました!今後、この座標系の平行移動と回転移動を使ったジェネラティブアートについて、紹介する予定です。









コメントを残す