前回の記事で、ニュートンの冷却法則の解析解を求めましたが、その導出過程で、対数logの公式を使っています。
この記事では、補足として次に示した対数logの公式を2つ紹介します。
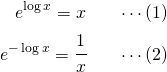
目次
公式(1)の証明
まず、![]() と置きます。両辺の対数logをとると、
と置きます。両辺の対数logをとると、
![]()
と式変形できます。したがって、y=xであることが分かりますので、公式(1)が正しいことが証明できました。
公式(2)の証明
公式(1)の証明と同じように、まず、![]() と置きます。さらに両辺の対数logをとると、
と置きます。さらに両辺の対数logをとると、
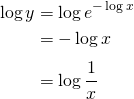
と式変形できます。したがって、y=1/xであるので、公式(2)が正しいことが証明できました。








コメントを残す