ベルヌーイの定理を簡単に導出する方法を考えてみました!
目次
ベルヌーイの定理 導出まで
一般的によく知られているベルヌーイの定理は、いくつかの仮定のもとで成り立つということに注意しなくてはなりません。ここでは次の4つの仮定をして、流体の運動方程式からベルヌーイの定理を導きます。
- 非圧縮
- 非粘性
- 定常流れ
- 1次元(流線上で成り立つ)
非圧縮性流体の運動を記述する「ナビエ・ストークス方程式」は、次のような方程式です。ここでは外力を考慮していません。
(1) ![]()
この式の左辺は「慣性項」と呼ばれ、第1項は「時間微分項」で、第2項は「移流項」です。右辺第1項は「圧力項」、第2項は「粘性項」と呼ばれます。
左辺の「移流項」は「非線形項」とも呼ばれ、速度が小さいときにはこれを無視することができます。この場合の流れを「ストークス流れ」と言います。
非粘性・定常状態を仮定すると
(2) ![]()
(3) ![]()
なので、(1)式は次のように簡単になります。
(4) ![]()
さらに、1次元(流線上)であることを仮定すると、
(5) ![]()
となります。(5)式の左辺は、次のように式変形できます。
(6) 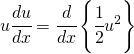
(5)式の項をまとめて、両辺にρをかければ、
(7) 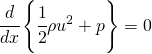
という式になります。この式は、左辺の{}内の物理量が位置によらず一定値であることを示しています。したがって、次のように表すこともできます。
(8) ![]()
これは一般的によく知られているベルヌーイの定理ですね。左辺の第1項は運動エネルギーを表していて「動圧」、左辺の第2項の圧力は「静圧」と呼ばれます。これらの和を「全圧」または「総圧」といいます。つまり、ベルヌーイの定理は動圧と静圧の和(全圧)が一定になることを示していて、速度が速くなると圧力が下がり、速度が遅くなると圧力が高くなることを意味しています。
ベルヌーイの定理 応用
ピトー管の原理
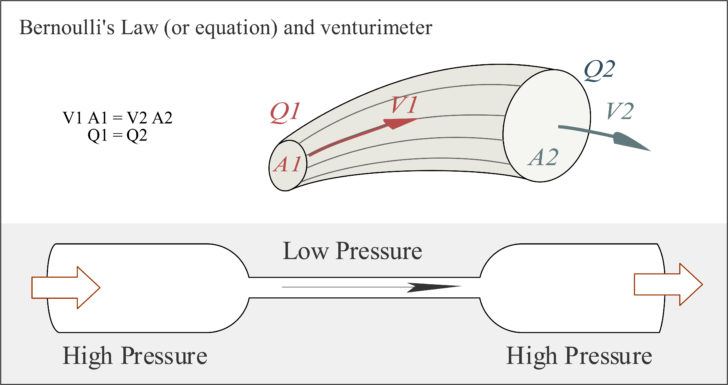
ピトー管とは、流体の流れの速さを測定するための計測器です。
ベルヌーイの定理は全圧が一定になることを示していますので、ある2点の全圧が等しくなると考えて、次のようにも表せます。
(9) ![]()
流れの中に物体をおくと、前面の1点で流速がゼロとなります。この点はよどみ点と呼ばれ、この点の圧力を![]() とすれば、
とすれば、
(10) ![]()
となります。![]() は物体の影響を受けない上流での圧力と速度ですが、言い換えれば物体がないとした場合のその点での圧力と速度でもあります。したがって、流れをせき止めることによる圧力の上昇は、
は物体の影響を受けない上流での圧力と速度ですが、言い換えれば物体がないとした場合のその点での圧力と速度でもあります。したがって、流れをせき止めることによる圧力の上昇は、
(11) ![]()
となります。これが動圧の意味です。これに対して、![]() が静圧、
が静圧、![]() が全圧ということになります。全圧と静圧の差から速度を測定することができますが、これがピトー管の原理です。
が全圧ということになります。全圧と静圧の差から速度を測定することができますが、これがピトー管の原理です。
プレーリードッグの巣の換気

プレーリードッグの巣穴は一方のマウンドは高く、他方は低く作られています。これは偶然などでなく、プレーリードッグは、マウンドの高さを意図的に変えていると言われています。マウンドの上を通り過ぎる風は、マウンドに押し上げられて風速が上がり、穴付近の圧力は低くなります。この原理を利用して、2つの出入り口に圧力差をつけることで、空気が効率的に流れるようにして巣穴の中に風を引き込んでいます。プレーリードッグがベルヌーイの定理を知っているとは思えませんが、少なくとも経験的にベルヌーイの定理を利用する方法を知っていたと考えられます。
さらに、プレーリードッグはかなり複雑な言語でコミュニケーションをとるとも言われており、非常に興味深いです。可愛いだけではないですね。
まとめ
この記事ではベルヌーイの定理の導出と簡単な応用例を紹介しました。今後、プレーリードッグの巣の換気システムを、流体シミュレーションで確認してみたいと考えています。(できるかは分かりませんが……)
ところで、プレーリードッグはどこに行けば見られるのでしょうか?知っていたら教えてほしいです!!


コメントを残す