目次
フラクタルとは
フラクタルは1975年にブノワ・マンデルブロによって提唱された幾何学の概念です。マンデルブロの有名な著書「フラクタル幾何学」では、フラクタルは「複数の部分に分割可能な断片化された大まかな幾何学形状で、それぞれが全体を縮小した複製である」と定義されています。最もよく知られているフラクタルパターンの1つがマンデルブロ自身の名前をとった「マンデルブロ集合」だと思います。この記事のアイキャッチ画像がそのマンデルブロ集合です。
ちなみに、マンデルブロがフラクタルを提唱する以前から、フラクタル図形に相当するものはすでに提案されていましたが、「数学の怪物」と呼ばれて人々の興味を引くことはありませんでした。
再帰関数
再帰
同じ規則を繰り返し繰り返し適用することによって、連続的な結果が得られることを「再帰」と呼びます。下記のコードのように自身を呼び出す関数は「再帰関数」と呼ばれ、特定の問題を解決するのに役立ちます。
1 2 3 | recFunction() { recFunction(); } |
階乗
整数nの階乗は次のように定義されます。
(1) 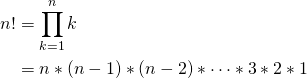
forループを使って階乗を計算するプログラムを書くと、次のようになります。
1 2 3 4 5 6 7 | int factorial(int n) { int f = 1; for (int i=0; i<n; i++) { f = f * (i+1); } return f; } |
この計算を再帰関数で表現することはできないでしょうか?ここでもう一度(1)式を見てみましょう。(1)式は次のように式変形していくことができます。
(2) 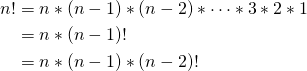
つまり、nの階乗はnにn-1の階乗を掛けたものということです。1を引いて階乗を計算する関数を再帰的に呼び出せば良いので、階乗を計算する再帰関数は次のようになります。forループを使わずにシンプルに表現できます。
1 2 3 4 5 6 7 | int factorial(int n) { if (n==1) { return 1; } else { return n * factorial(n-1); } } |
カントール集合
カントール集合は図形としての面白みはありませんが、フラクタルの入門としては良い例です。
- 線を描く
- 線を3等分して中央を取り除く
- 残った線に対してもそれぞれ②の処理をする
先ほど紹介した再帰関数を使ってProcessingでカントール集合を表現してみます。次にコードとその実行結果を示します。線の色は何となくランダムにしてみました。
<コード>
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | void setup() { size(729, 400); background(255); cantor(0, 0, 729); } void draw() { noLoop(); } void cantor(float x, float y, float len) { float h = 60; color fillcol = color(random(255),random(255),random(255)); if (len >= 1) { noStroke(); fill(fillcol); rect(x, y, len, h/2); y += h; cantor(x, y, len/3); cantor(x+len*2/3, y, len/3); } } |
<実行結果>
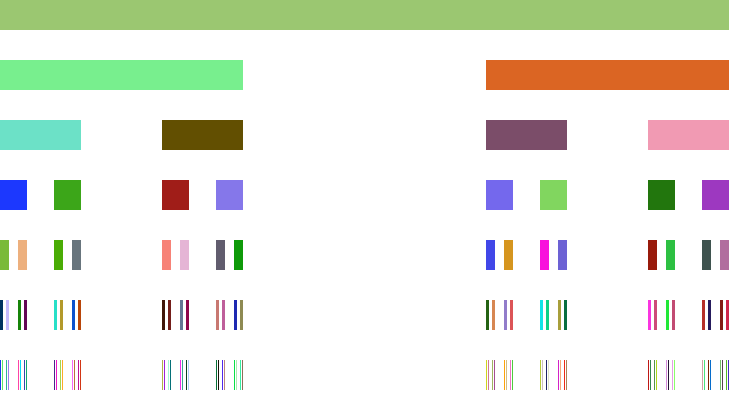
まとめ
今回の記事では、再帰関数とフラクタルの入門としてカントール集合を紹介しました。今後もProcessingで色々なフラクタル図形を作成して紹介していきます!







コメントを残す