前々回の記事では、ニュートンの冷却法則の解析解を導出しました。今回の記事では、いよいよ数値計算によって解を求めます!
目次
オイラー法
オイラー法とは、常微分方程式の数値解を求めるアルゴリズムの1つです。対象とする微分方程式を差分方程式に書き換えて、微分方程式の数値解を求める標準的な方法です。
オイラーのアルゴリズム
オイラーのアルゴリズムを理解するために、ここでは次の1階微分方程式について考えます。
(1) ![]()
たとえば、![]() において
において![]() の値は
の値は![]() であるとします。式(1)から
であるとします。式(1)から![]() における
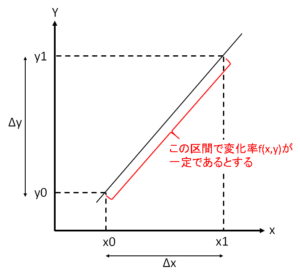
における![]() の傾き(どのように変化するか)がわかりますので、xの変化
の傾き(どのように変化するか)がわかりますので、xの変化![]() が十分に小さいとき、
が十分に小さいとき、![]() における
における![]() の近似値を求めることができます。ここでは、
の近似値を求めることができます。ここでは、![]() の
の![]() についての変化率
についての変化率![]() が
が![]() から
から![]() までの区間で一定であるとします。この仮定により、
までの区間で一定であるとします。この仮定により、![]() における
における![]() の近似値は次のように与えられます。
の近似値は次のように与えられます。
(2) ![]()
これを一般化するれば、任意の点![]() における
における![]() の近似値は漸化式
の近似値は漸化式
(3) ![]()
で計算することができます。この方法をオイラー法といいます。
ニュートンの冷却法則の数値解
では次にニュートンの冷却法則の数値解をオイラー法を使って求めてみます。前々回の記事で書きましたが、この法則を表す微分方程式と解析解は以下のとおりです。
(4) ![]()
(5) ![]()
数値解を求めたい(4)式にオイラー法を適用すると、次のようになります。
(6) ![]()
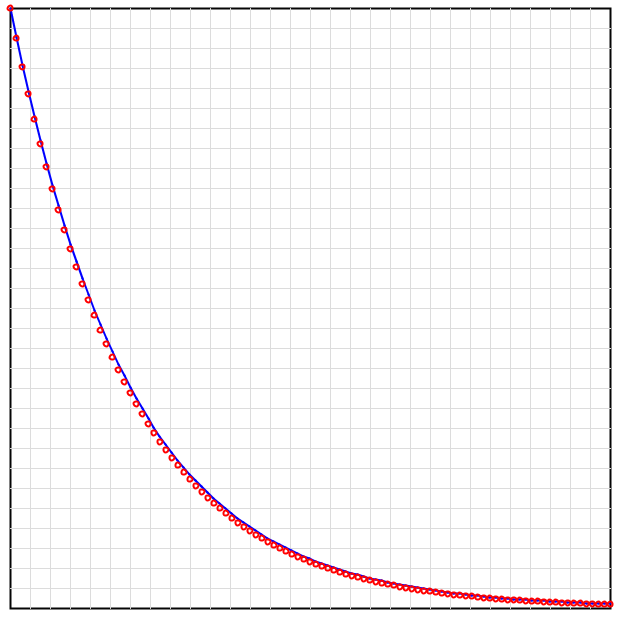
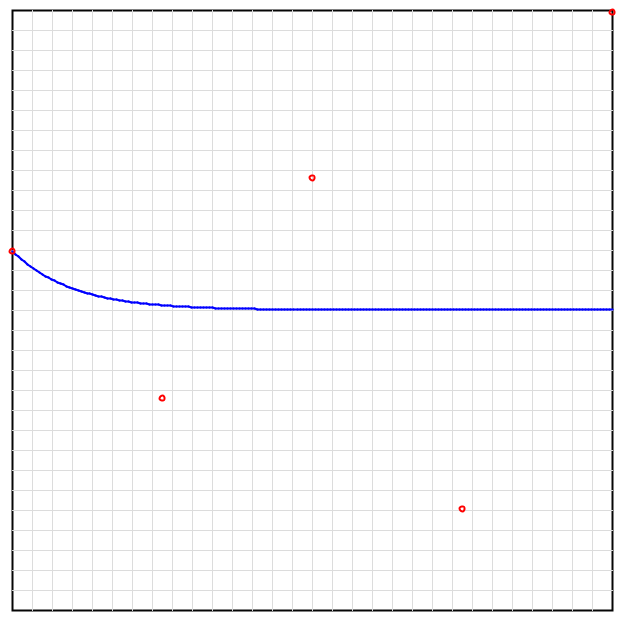
この式を数値的に解けば、(5)式の解が得られるはずです。今回は、以前の記事で扱ったProcessingで数値計算とグラフ作成をしました。以下に解析解と数値計算の結果を比較して示します。各パラメータは、![]() としました。
としました。
グラフの青い実線が解析解(5)式、赤いプロットが数値計算の結果になります。オイラー法による数値計算の結果が解析解とよく一致しています。
数値計算の安定性
次にパラメータ![]() を変化させていったときの結果を示します。
を変化させていったときの結果を示します。
【![]() の結果】
の結果】
 【
【![]() の結果】
の結果】
 【
【![]() の結果】
の結果】
なぜこのような結果になるか、オイラー法のアルゴリズムから考察してみます。
まず、(6)式に今回設定したパラメータを代入します。![]() なので、
なので、
(7) ![]()
となります。次にそれぞれのΔtの場合について考えていきます。
Δt=1.0のとき
このとき、(7)式は次のようになります。
(8) ![]()
つまり、初期の![]() 以外はすべてゼロになるということです。先ほどグラフで示したように、Δtを1.0まで大きくすると、解析解の曲線を再現できない、ということです。Δtを大きくしすぎると、数値計算では誤差が大きくなってしまいますので、条件の設定には注意が必要です。
以外はすべてゼロになるということです。先ほどグラフで示したように、Δtを1.0まで大きくすると、解析解の曲線を再現できない、ということです。Δtを大きくしすぎると、数値計算では誤差が大きくなってしまいますので、条件の設定には注意が必要です。
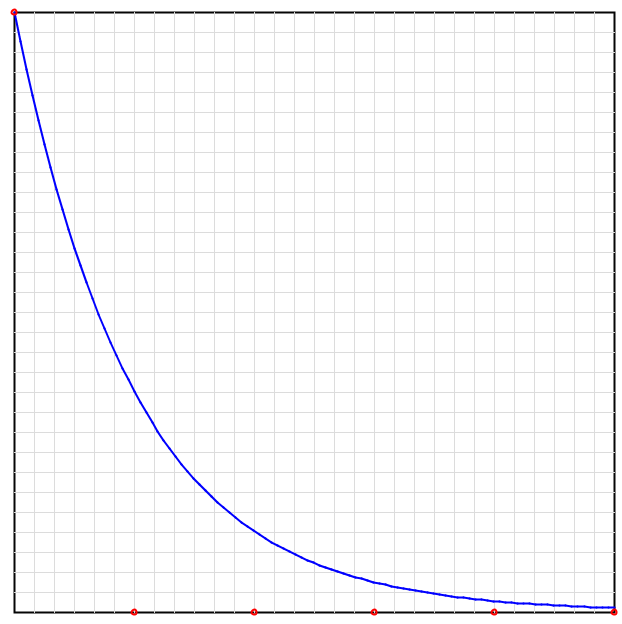
Δt=2.0のとき
このとき、(7)式は次のようになります。
(9) ![]()
これは![]() の絶対値は初期状態
の絶対値は初期状態![]() から変わらず、符号が反転し続けることを示しています。グラフの赤いプロットで示したように、数値計算の解は振動し続けます。
から変わらず、符号が反転し続けることを示しています。グラフの赤いプロットで示したように、数値計算の解は振動し続けます。
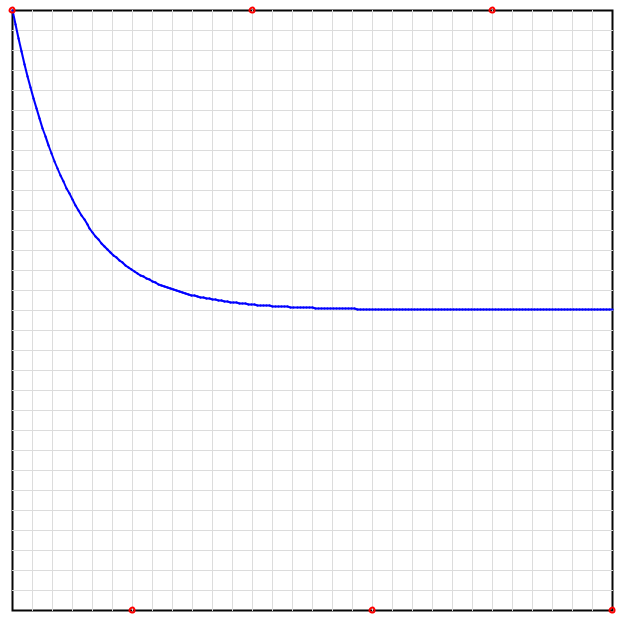
Δt=2.5のとき
このとき、(7)式は次のようになります。
(10) ![]()
これは![]() の絶対値は初期状態
の絶対値は初期状態![]() から増加し続けて、符号も反転し続けることを示しています。このような状態を数値不安定といいます。この状態になると、変数の値が発散して、エラーが起きます。
から増加し続けて、符号も反転し続けることを示しています。このような状態を数値不安定といいます。この状態になると、変数の値が発散して、エラーが起きます。
まとめ
オイラー法によってニュートンの冷却法則の微分方程式を数値計算で解きました。数値計算を使えば、複雑な微分方程式を解くこともできます。ただし、今回の記事で扱ったように、パラメータの設定によっては誤差が大きくなったり、振動や発散が起きてしまいます。数値計算で得られた結果が妥当なものであるか、確認する必要があります。
今後は、他の物理現象に数値計算を適用した例や、オイラー法以外の数値計算のアルゴリズムを紹介していきます!








コメントを残す