今回は、Processingで乱数を使って遊んでみました!
目次
Processingで乱数生成
乱数とは、サイコロの出目のように規則性がなく、予測できない数値のことです。この記事では、一様乱数、正規乱数、パーリンノイズを扱います。
一様乱数の生成
さっそくProcessingのrandom関数を使って乱数を生成してみます。random関数は呼び出すたびに異なる数値を返します。パラメータで値の上限、または範囲を指定することもできます。例えば、random(10)とすれば、0~10の乱数が生成されます。
次にrandom関数を使ったコードの例と実行結果を示します。このコードでは、500個の乱数を生成して、その結果を折れ線グラフとして表示します。
【コード】
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | void setup() { size(500,300); smooth(); } void draw() { background(255); noFill(); strokeWeight(1.0); beginShape(); for (int x = 0; x < width; x++) { float y = random(height); vertex(x,y); } endShape(); noLoop(); } void keyPressed() { if (key == 'p') { save("graph.png"); } } |
【実行結果】
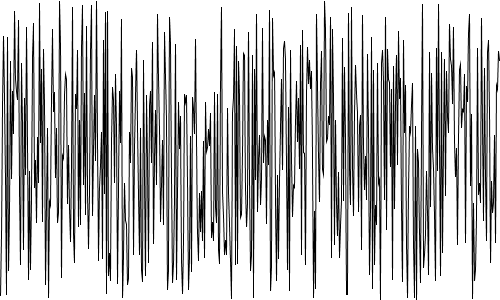
Processingのrandom関数は、数値を均等に生成します。生成された乱数の分布を棒グラフで図示して確認してみます。
次のコードでは、0~9の整数の乱数を生成して、配列romCountsで出現頻度をトラッキングします。その結果を棒グラフで図示します。また具体的な数値データは”output.csv”というcsvファイルに出力されますので、エクセル等を使って標準偏差や変動係数を算出することができます。
【コード】
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | float[] romCounts; PrintWriter file; void setup() { file = createWriter("output.csv"); size(640,360); romCounts = new float[10]; } void draw() { int index = int(random(romCounts.length)); romCounts[index]++; stroke(0); strokeWeight(1); fill(255,3,19); int w = width / romCounts.length; for (int x = 0; x < romCounts.length; x++) { rect(x*w, height-romCounts[x], w, romCounts[x]); } } void keyPressed() { if (key == 'p') { save("graph.png"); } if (key == 'q') { for (int x = 0; x < romCounts.length; x++) { file.println(romCounts[x]); } file.flush(); file.close(); exit(); } if (key == 't') { noLoop(); } if (key == 's') { loop(); } } |
【実行結果】
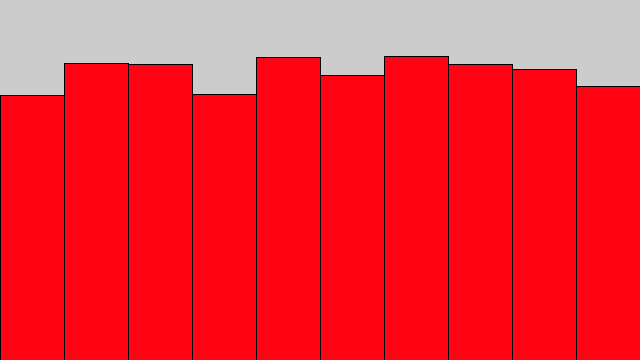
このグラフの棒の高さは均等になっていませんね。これはサンプル数が比較的少ないため、各乱数が生成された回数にバラツキがあることを示しています。高度な乱数ジェネレータでは、サンプル数が多くなければ、頻度が均等になっていきます。
正規乱数の生成
平均付近に集中するような値の分を正規分布と呼びます。Processingでは、Randomクラスを利用すれば正規乱数を生成することができます。このクラスを使うためには、最初にRandom型の変数を宣言した後、Randomオブジェクトを作成する必要があります。具体的な実装例を示します。
nextGaussian()関数が呼び出されるたびに、正規乱数が生成されます。この関数は、乱数の正規分布を返す際のパラメータとして、平均値0と標準偏差1を使用します。必要に応じて、調整する必要があります。
【コード】
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | import java.util.Random; Random generator; float[] romCounts; int csize=40; int dx=16; float sd=100; float mean=320; void setup() { size(640,640); generator = new Random(); romCounts = new float[csize]; } void draw() { float num = (float )generator.nextGaussian(); float x = sd * num + mean; int index = int(x) / dx; if (index >= 0 && index < csize) { romCounts[index]++; } stroke(0); strokeWeight(1); fill(255,3,19); int w = width / romCounts.length; for (int xx = 0; xx < romCounts.length; xx++) { rect(xx*w, height-romCounts[xx], w, romCounts[xx]); } } void keyPressed() { if (key == 'p') { save("graph.png"); } if (key == 'q') { exit(); } } |
【実行結果】
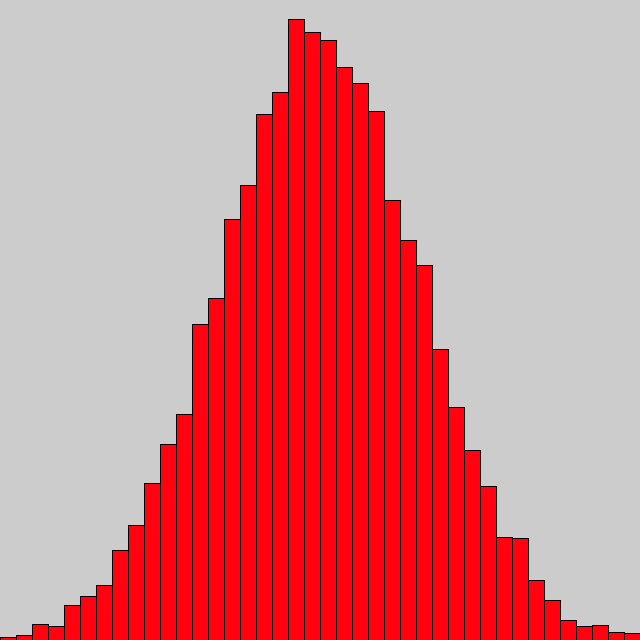
平均値(今回はグラフの中心)が最も頻度が高く、平均値から外れるほど頻度が低くなっていくことが分かります。
パーリンノイズ
パーリンノイズは、コンピュータ・グラフィックスのリアリティを向上させるために使われているテクスチャの作成技法です。パーリンノイズを使うと、雲や風景、大理石のようなパターン化されたテクスチャなど自然な性質をもった様々なエフェクトを生成できます。
Processingには、noise()という名前の関数としてパーリンノイズアルゴリズムが実装されています。noise()では出力範囲が固定されていて、常に0~1の範囲の値が返されます。
次のコードは、noise()関数で生成した乱数を1次元のグラフにするという簡単なものです。今回は、noise()関数の引数となるtのインクリメントの幅dtを変更して、グラフを比較してみました。
【コード】
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | float dt=1.0; //float dt=0.1; //float dt=0.01; //float dt=0.001; void setup() { size(400,300); smooth(); } void draw() { float t=0; background(255); noFill(); stroke(255,0,0); strokeWeight(1); beginShape(); for (int i = 0; i < width; i++) { float y = noise(t)*height; t += dt; vertex(i,y); } endShape(); noLoop(); } void keyPressed() { if (key=='p') { save("graph.png"); } } |
【実行結果】
・dt=1.0の結果
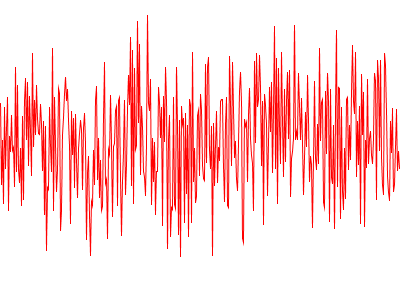
・dt=0.1の結果
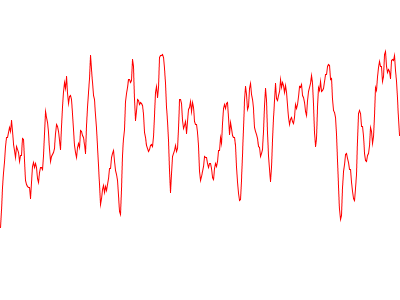
・dt=0.01の結果
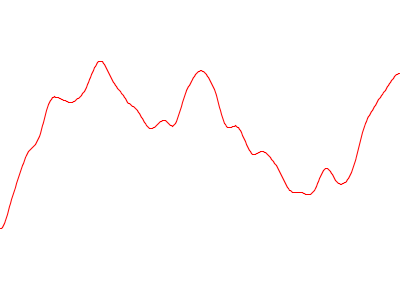
・dt=0.001の結果

これらの結果から、インクリメント幅dtを大きくすると、一様乱数と同様に認識できるパターンのない乱数列が生成され、dtを小さくすると、乱数が緩やかに変化していくスムーズな乱数列が生成されていることが分かります。
2次元のノイズ
2次元のノイズも1次元のノイズと考え方は基本的に同じです。違うのは、1次元の線に沿った値ではなく、グリッド上にある値を使うことです。ここでは、すべてのピクセルにランダムな明度を指定するプログラムを作成してみました。まずは一様乱数で明度を指定する例を示します。
【コード】
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | void setup() { size(300,300); } void draw() { loadPixels(); for (int x = 0; x < width; x++) { for (int y = 0; y < height; y++) { float gs = random(255); pixels[y*width+x] = color(gs); } } updatePixels(); noLoop(); } |
【実行結果】

一様乱数で明度を指定すると、値が飛び飛びになるので、テレビの砂嵐のようになります。明度の変化を滑らかにしたければ、パーリンノイズによって生成された乱数を使います。noise()関数では0~1の範囲の乱数が返されることに注意してください。
【コード】
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | void setup() { size(300,300); } void draw() { float xn = 0.0; float dx = 0.01; float dy = 0.01; loadPixels(); for (int x = 0; x < width; x++) { float yn = 0.0; for (int y = 0; y < height; y++) { float gs = map(noise(xn,yn),0,1,0,255); pixels[y*width+x] = color(gs); yn += dy; } xn += dx; } updatePixels(); noLoop(); } |
【実行結果】

隣接するピクセルの明度の変化が小さくなり、雲のような画像になりました。このように、乱数の生成方法によって、結果を大きく変化させることができます。
まとめ
この記事では、Processingで乱数を生成する方法を紹介しました。乱数の生成方法によって、結果を大きく変化させられるので、これを活用すれば様々な画像やアニメーションを作成できそうです。
今後も色々と試していこうと思います!







コメントを残す